Basic Knowledge for Ab-initio Calculation in Materials' Sciences: Birch

In continuum mechanics, an equation of state suitable for modeling solids is naturally rather different from the ideal gas law. A solid has a certain equilibrium volume $V 0$ , and the energy increases quadratically as volume is increased or decreased a small amount from that value. The simplest plausible dependence of energy on volume would be a harmonic solid, with

$E = E_0 + \frac{1}{2} B_0 \frac{(V-V_0)^2}{V_0}.$

The next simplest reasonable model would be with a constant bulk modulus

$B = - V \left( \frac{\partial P}{\partial V} \right)_T. (2)$

$E = E_0 + B_0 \left( V_0 - V + V \ln(V/V_0) \right).$

Murnaghan equation of state

A more sophisticated equation of state was derived by Francis D. Murnaghan of Johns Hopkins University in 1944^[1]. To begin with, we consider the pressure

$P = - \left( \frac{\partial E}{\partial V} \right)_S (1)$

and the bulk modulus

$B = - V \left( \frac{\partial P}{\partial V} \right)_T. (2)$

Experimentally, the bulk modulus pressure derivative

$B' = \left( \frac{\partial B}{\partial P} \right)_T (3)$

is found to change little with pressure. If we take $B' = B' 0$ to be a constant, then

B = B 0 + B' 0 P (4)

where $B 0$ is the value of $B$ when $P = 0.$ We may equate this with (2) and rearrange as

$\frac{d V}{V} = -\frac{d P}{B_0 + B'_0 P}. (5)$

Integrating this results in

$P(V) = \frac{B_0}{B'_0} \left(\left(\frac{V_0}{V}\right)^{B'_0} - 1\right) (6)$

or equivalently

$V(P) = V_0 \left(1+B'_0 \frac{P}{B_0}\right)^{-1/B'_0}. (7)$

Substituting (6) into 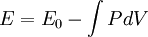$E = E_0 - \int P dV$ then results in the equation of state for energy.

$E(V) = E_0 + \frac{ B_0 V }{ B_0' } \left( \frac{ (V_0/V)^{B_0'} }{ B_0' - 1 } + 1 \right) - \frac{ B_0 V_0 }{ B_0' - 1 }. (8)$

Many substances have a fairly constant $B' 0$ of about 3.5.

Birch–Murnaghan equation of state

The third-order Birch–Murnaghan isothermal equation of state, published in 1947 by Francis Birch of Harvard^[2], is given by:

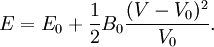
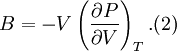
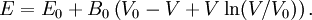
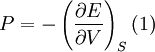
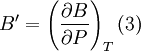
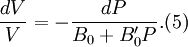
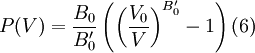
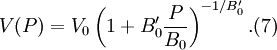
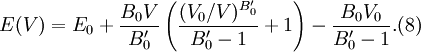
$P(V)=\frac{3B_0}{2} \left[\left(\frac{V_0}{V}\right)^\frac{7}{3} - \left(\frac{V_0}{V}\right)^\frac{5}{3}\right] \left\{1+\frac{3}{4}\left(B_0^\prime-4\right) \left[\left(\frac{V_0}{V}\right)^\frac{2}{3} - 1\right]\right\}$

Again, E(V) is found by integration of the pressure:

$E(V) = E_0 + \frac{9V_0B_0}{16} \left\{ \left[\left(\frac{V_0}{V}\right)^\frac{2}{3}-1\right]^3B_0^\prime + \left[\left(\frac{V_0}{V}\right)^\frac{2}{3}-1\right]^2 \left[6-4\left(\frac{V_0}{V}\right)^\frac{2}{3}\right]\right\}$

References

^ F.D. Murnaghan, 'The Compressibility of Media under Extreme Pressures', in Proceedings of the National Academy of Sciences, vol. 30, pp. 244-247, 1944.