Potential of a Uniform Sphere of Charge

The use of Poisson's and Laplace's equations will be explored for a uniform sphere of charge. In spherical polar coordinates, Poisson's equation takes the form:

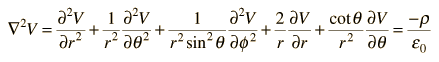
but since there is full spherical symmetry here, the derivatives with respect to θ and φ must be zero, leaving the form 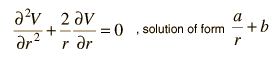Examining first the region outside the sphere, Laplace's law applies.

Since the zero of potential is arbitrary, it is reasonable to choose the zero of potential at infinity, the standard practice with localized charges. This gives the value b=0. Since the sphere of charge will look like a point charge at large distances, we may conclude that

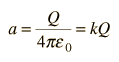
so the solution to LaPlace's law outside the sphere is

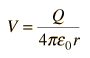
Now examining the potential inside the sphere, the potential must have a term of order r² to give a constant on the left side of the equation, so the solution is of the form

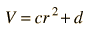
Substituting into Poisson's equation gives

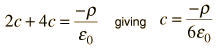
Now to meet the boundary conditions at the surface of the sphere, r=R

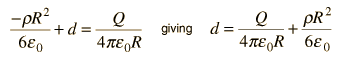
The full solution for the potential inside the sphere from Poisson's equation is

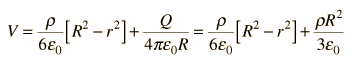
Reference: http://hyperphysics.phy-astr.gsu.edu/hbase/electric/laplace.html#c2