Lattice Structures in Crystalline Solids
........
.......


 .
.
To continue reading click on the link below:
https://opentextbc.ca/chemistry/chapter/10-6-lattice-structures-in-crystalline-solids/
.......
Calculation of Ionic Radii
If we know the edge length of a unit cell of an ionic compound and the position of the ions in the cell, we can calculate ionic radii for the ions in the compound if we make assumptions about individual ionic shapes and contacts.
Example 5
Calculation of Ionic Radii
The edge length of the unit cell of LiCl (NaCl-like structure, FCC) is 0.514 nm or 5.14 Å. Assuming that the lithium ion is small enough so that the chloride ions are in contact, as in Figure 15, calculate the ionic radius for the chloride ion.
The edge length of the unit cell of LiCl (NaCl-like structure, FCC) is 0.514 nm or 5.14 Å. Assuming that the lithium ion is small enough so that the chloride ions are in contact, as in Figure 15, calculate the ionic radius for the chloride ion.
Note: The length unit angstrom, Å, is often used to represent atomic-scale dimensions and is equivalent to 10−10 m.
Solution
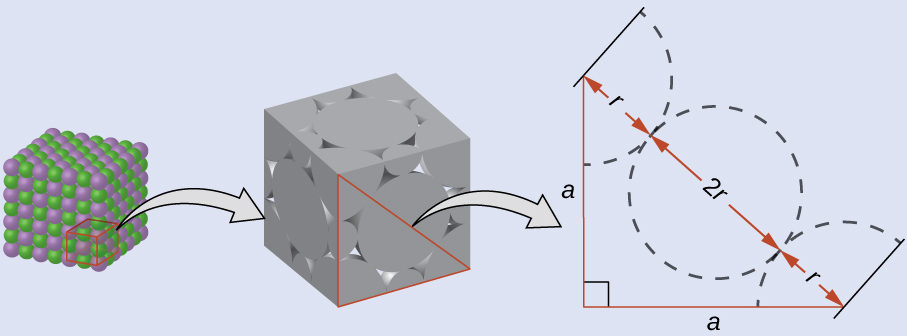
On the face of a LiCl unit cell, chloride ions contact each other across the diagonal of the face:
On the face of a LiCl unit cell, chloride ions contact each other across the diagonal of the face:

Drawing a right triangle on the face of the unit cell, we see that the length of the diagonal is equal to four chloride radii (one radius from each corner chloride and one diameter—which equals two radii—from the chloride ion in the center of the face), so d = 4r. From the Pythagorean theorem, we have:
which yields:
Solving this gives:
Check Your Learning
The edge length of the unit cell of KCl (NaCl-like structure, FCC) is 6.28 Å. Assuming anion-cation contact along the cell edge, calculate the radius of the potassium ion. The radius of the chloride ion is 1.82 Å.
The edge length of the unit cell of KCl (NaCl-like structure, FCC) is 6.28 Å. Assuming anion-cation contact along the cell edge, calculate the radius of the potassium ion. The radius of the chloride ion is 1.82 Å.
Answer:
The radius of the potassium ion is 1.33 Å.
It is important to realize that values for ionic radii calculated from the edge lengths of unit cells depend on numerous assumptions, such as a perfect spherical shape for ions, which are approximations at best. Hence, such calculated values are themselves approximate and comparisons cannot be pushed too far. Nevertheless, this method has proved useful for calculating ionic radii from experimental measurements such as X-ray crystallographic determinations.
To continue reading click on the link below:
https://opentextbc.ca/chemistry/chapter/10-6-lattice-structures-in-crystalline-solids/







No comments