Simple and Detailed Presentation of the DFT theory and the LAPW Method for Ab initio Calculation
First we will begin with the presentation of the Taylor Expanson.
Why do we proceed to replace a function by a polynomial expansion as in Taylor Expanson?
What's the raison?
Simply because the original functions are difficult to solve even numerically. For the functions solved numerically, there is a big problem which is the convergence problem because there is some functions which converge with difficulty and other which they never converge.
For more information about the Taylor expansion of some functions check the following links:
https://www.mathsisfun.com/algebra/taylor-series.html
http://tutorial.math.lamar.edu/Classes/CalcII/TaylorSeries.aspx
https://www.sciencedirect.com/science/article/pii/B9780080129037500091
To know the Applications of Taylor Series check the following link:
http://sces.phys.utk.edu/~moreo/mm08/fosso.pdf
To solve numerically the polynomial functions, there are many methods as at the following links:
http://compmath-journal.org/dnload/Robin-Kumar-and-Vipan-/CMJV06I06P0290.pdf
To study the convergence of the numerical methods check the following links:
http://web.mit.edu/16.90/BackUp/www/pdfs/Chapter2.pdf
https://www.quora.com/What-is-the-meaning-of-Divergent-And-Convergent-in-Numerical-Method-i-e-in-Gauss-Seidel-Method
https://math.stackexchange.com/questions/2656855/how-to-select-convergence-criterion-in-numerical-analysis
Second we will talk about the basis functions and the basis sets.
Basis Functions: All the functions to be used to solve numerically the equations of the atomic and molecular systems or solid systems. The basis functions are one-electron functions and they are frequently called orbitals because each one-electron function represent an orbital with both spins.
Ex1: In atomic and molecular systems
- Slater-type functions or orbitals STO
- Gaussian-type functions or orbitals GTO
- Laguerre functions
NB: Both the STO and GTO are used individually to do atomic calculations on the atom of Hydrogen.
Ex2: In solid systems
- Plane waves
- Spherical harmonics
Basis set: The sufficient number of basis functions to represent all parts of systems
Ex1: In atomic and molecular systems
- A basis set formed only of Slater-type functions or orbitals
- A basis set formed only of Gaussian-type functions or orbitals
Difference between the Slater-type functions and the Gaussian-type functions:
- The Slater-type functions have a physical meaning but are very difficult to calculate.
- The Gaussian-type functions have no physical meaning but are easy to calculate.
The solution:
Create a Slater-type functions as an expansion of Gaussian-type functions.
For more information check the following link:
http://www.helsinki.fi/kemia/fysikaalinen/opetus/jlk/luennot/Lecture5.pdf
Ex2: In solid systems
- A basis set formed only of the plane waves as in the pseudopoential methods
- A basis set formed of the plane waves and spherical harmonics as in the all-electron methos (ex: LAPW).
NB: In the scond case, to ensure the continuity at the sphere's surface, we have to proceed to expand the plane waves as an expansion of the spherical harmonics. Check this file at the page 19 http://susi.theochem.tuwien.ac.at/reg_user/textbooks/DFT_and_LAPW-2_cottenier.pdf
To get more information on the basis functions and the basis sets check the following links:
http://vergil.chemistry.gatech.edu/courses/chem6485/pdf/basis-sets.pdf
http://folk.uio.no/helgaker/talks/SostrupBasis_10.pdf
http://shodor.org/succeed-1.0/programs/compchem98/labs/settime/
Basis functions and basis sets in euclidean space
In euclidean space, we can use the vectors i,j and k to represent any vector in the plane or in the space. Thus, the three vectors are the basis vectors. To represent any vector in a plane, we need only two vectors i and j or i and k or j and k; so the basis set is formed only of two vectors. and to represent a vector in the space, we need the three vectors; so the basis set is formed of three vectors.
Third we talk about the DFT theory.
Eks: Kohn-Sham total energy Eks = T + V ----> (1)
T: Total cinetic energy (elctrons and nucleus) T = Te + Tn -----> (2)
Tn = 0 ------> (3) according to Born-Openheimer Approximation
V: total potential energy (electrons and nucleus ) V = Ve + Vn -----> (4)
Vn = Vext ------> (5) is called the exterior potential energy
Eh: Hartree total energy Eh = To + Vh ------> (6)
To: Total energy of non-intercting electrons Vh: Hartree potential energy (partial correlation contribution)
Ehf: Hartree-Fock total energy Ehf = To + Vh + Vx ----> (7)
Vx: Fock Exchange potential energy Ehf = Eh + Vx -----> (8)
From the equations (1), (2), (3) and (4) we get the following equation:
Eks = Te + Ve + Vext ------> (9)
Relation between Eks and Ehf
Eks = Ehf + Vc + Vext ------> (10)
Vc: Part of correlation which is absent in Hartree potential energy
From (9) and (10) we get the following rquation:
Eks = To + Vh + Vx + Vc + Vext -----------> (11)
We put Vxc = Vx + Vc ------> (12)
Vxc: is called Exchange-Correlation Energy
Vc: Correlation energy and is a kinetic energy in reality.
Vx: Exchange energy and is a potential energy and in reality is a correlation effect due to the Pauli exclusion principle which exclude the elctrons with the same spin to be in the same orbital.
NB: The meaning of correlation and exchange is convential and not real.
We put Veff = Vh + Vxc + Vext -------> (13)
Veff: is called the effective potential energy despite it contains some of the kinetic energy of correlation.
From (11), (12) and (13) we get the following equation:
Eks = To + Veff -------> (14)
From (9) and (11) we get that Vc = Te - To ----> (15)
and Vx = Ve - Vh ------> (16)
We know, according to the DFT theory, that all of the energies are related to the electron density; thus the final equation will be as follows:
Eks(rho) = To(rho) + Vh(rho) + Vxc(rho) + Vext(rho) --- > (17)
The exact ground state electron dnsity can be formulated as follows:
where the single-particle wave functions φi(~r) are the N lowest-energy solutions of the KohnSham equation:
And now we did won a lot. To find the ground-state density, we don’t need to use the second Hohenberg-Kohn theorem any more, but we can rely on solving familiar Schr¨odinger-like noninteracting single-particle equations. The alternative of using the regular Schr¨odinger equation, would have led to a far more difficult system of coupled differential equations, because of the electron-electron interaction.
Be aware that the single-particle wave functions φi are not the wave functions of electrons! They describe mathematical quasi-particles, without a direct physical meaning. Only the overall density of these quasi-particles is guaranteed to be equal to the true electron density. Also the single-particle energies ²i are not single-electron energies.
-----------------------------------------------------------------------------------------------------------
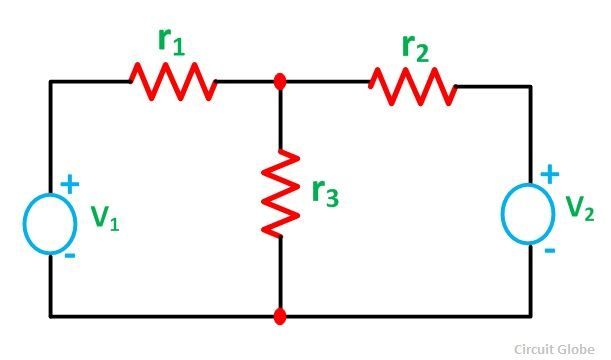
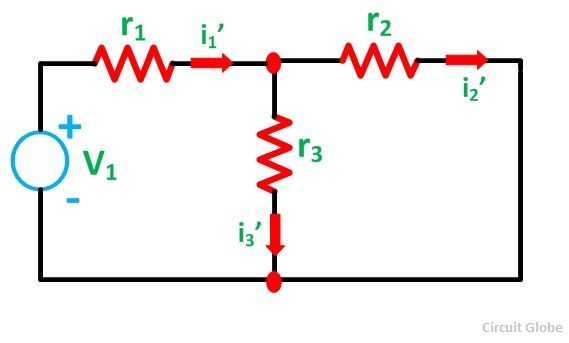
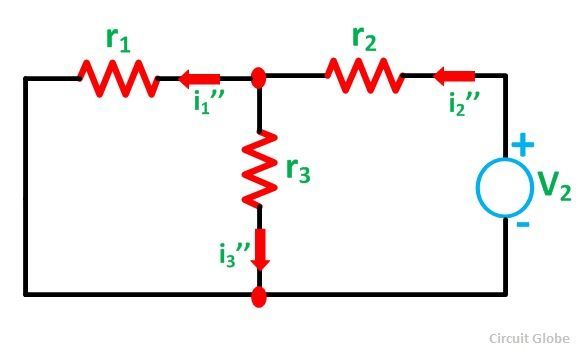
The previous statement is similar to what happennes in the superposition theorem in electrical circuits.
The real current is i1 and both i1(prime) and i1(second) are virtal currents which allow to calculate the real current.
reference: https://circuitglobe.com/what-is-superposition-theorem.html
--------------------------------------------------------------------------
Both the Hartree operator VH and the exchange-correlation operator Vxc depend on the density ρ(~r), which in turn depends on the φi which are being searched. This means we are dealing with a self-consistency problem: the solutions (φi) determine the original equation (VH and Vxc in HKS), and the equation cannot be written down and solved before its solution is known. An iterative procedure is needed to escape from this paradox (see fig. 1.1). Some starting density ρ0 is guessed, and a hamiltonian HKS1 is constructed with it. The eigenvalue problem is solved, and results in a set of φ1 from which a density ρ1 can be derived. Most probably ρ0 will differ from ρ1. Now ρ1 is used to construct HKS2, which will yield a ρ2, etc. The procedure can be set up in such a way that this series will converge to a density ρf which generates a HKSf which yields as solution again ρf : this final density is then consistent with the hamiltonian.
Reference: http://susi.theochem.tuwien.ac.at/reg_user/textbooks/DFT_and_LAPW-2_cottenier.pdf
The exchange-correlation functional
The exchange-correlation part is the only unknown one in the Schrondinger equation. To calculate it, we need to make approximations. The most known approwimations are:
- Local Density Approximation (LDA):
This postulate is somehow reasonable: it means that the exchange-correlation energy due to a particular density ρ(~r) could be found by dividing the material in infinitesimally small volumes with a constant density. Each such volume contributes to the total exchange correlation energy by an amount equal to the exchange correlation energy of an identical volume filled with a homogeneous electron gas, that has the same overall density as the original material has in this volume (see Fig. 1.2). No law of nature guarantees that the true Exc is of this form, it is only a reasonable guess. By construction, LDA is expected to perform well for systems with a slowly varying density. But rather surprisingly, it appears to be very accurate in many other (realistic) cases too.
- Generalized Gradient Approximation (GGA):
A next logical step to improve on LDA, is to make the exchange-correlation contribution of every infinitesimal volume not only dependent on the local density in that volume, but also on the density in the neighbouring volumes. In other words, the gradient of the density will play a role. Although GGA performs in general slightly better than LDA, there are a few drawbacks. There is only one LDA exchange-correlation functional, because there is a unique definition for ²xc. But there is some freedom to incorporate the density gradient, and therefore several versions of GGA exist (first drawback). Moreover, in practice one often fits a candidate GGA-functional with (hopefully only a few) free parameters to a large set of experimental data on atoms and molecules. The best values for these parameters are fixed then, and the functional is ready to be used routinely in solids. Therefore such a GGA-calculation is strictly spoken not an ab initio calculation, as some experimental information is used (second drawback). Nevertheless, there exist GGA’s that are parameter free.
Reference: http://susi.theochem.tuwien.ac.at/reg_user/textbooks/DFT_and_LAPW-2_cottenier.pdf
Fourth we talk about how to solve the Schrodinger equations
Irrespective whether one has used HF or DFT as level 2 approximation, one ends up with an
infinite set of one-electron equations of the following type (m is an integer number that counts
the members of the set):
We call Hˆsp the single-particle hamiltonian. For HF, Vα is the exchange operator. The φm are true one-electron (or single-particle) orbitals for HF. Exchange is treated exactly, but correlation effects are not included at all. They can be added only in elaborations on the HF-method.
For DFT, Vα is the exchange-correlation operator, in the L(S)DA, GGA or another approximation. Exchange and correlation are both treated, but both approximately. The φm are mathematical single-particle orbitals (they are called quasi-particle orbitals).
The similarity between the Hartree-Fock and Kohn-Sham equations means that the same mathematical techniques can be used to solve them. ‘Solving’ in most methods means that we want to find the coefficients c m p needed to express φm in a given basis set φ b p :
The wave functions φm belong to a function space which has an infinite dimension, P is therefore in principle infinite. In practice one works with a limited set of basis functions. Such a limited basis will never be able to describe φm exactly, but one could try to find a basis that can generate a function that is ‘close’ to φm.
Continue reading on the page 9 of the following text book:
http://susi.theochem.tuwien.ac.at/reg_user/textbooks/DFT_and_LAPW-2_cottenier.pdf
Fiveth we talk about the different methods to solve the Kohn-Sham equations
Unlike the Pseudopotetial method which calculate only the valence electrons only, the All-electrons methods calculate the both the core and valence electrons. There are many all-electron methods; we focused those used in the wien2k code.
The APW Method:
Why do we proceed to replace a function by a polynomial expansion as in Taylor Expanson?
What's the raison?
Simply because the original functions are difficult to solve even numerically. For the functions solved numerically, there is a big problem which is the convergence problem because there is some functions which converge with difficulty and other which they never converge.
For more information about the Taylor expansion of some functions check the following links:
https://www.mathsisfun.com/algebra/taylor-series.html
http://tutorial.math.lamar.edu/Classes/CalcII/TaylorSeries.aspx
https://www.sciencedirect.com/science/article/pii/B9780080129037500091
To know the Applications of Taylor Series check the following link:
http://sces.phys.utk.edu/~moreo/mm08/fosso.pdf
To solve numerically the polynomial functions, there are many methods as at the following links:
http://compmath-journal.org/dnload/Robin-Kumar-and-Vipan-/CMJV06I06P0290.pdf
To study the convergence of the numerical methods check the following links:
http://web.mit.edu/16.90/BackUp/www/pdfs/Chapter2.pdf
https://www.quora.com/What-is-the-meaning-of-Divergent-And-Convergent-in-Numerical-Method-i-e-in-Gauss-Seidel-Method
https://math.stackexchange.com/questions/2656855/how-to-select-convergence-criterion-in-numerical-analysis
Second we will talk about the basis functions and the basis sets.
Basis Functions: All the functions to be used to solve numerically the equations of the atomic and molecular systems or solid systems. The basis functions are one-electron functions and they are frequently called orbitals because each one-electron function represent an orbital with both spins.
Ex1: In atomic and molecular systems
- Slater-type functions or orbitals STO
- Gaussian-type functions or orbitals GTO
- Laguerre functions
NB: Both the STO and GTO are used individually to do atomic calculations on the atom of Hydrogen.
Ex2: In solid systems
- Plane waves
- Spherical harmonics
Basis set: The sufficient number of basis functions to represent all parts of systems
Ex1: In atomic and molecular systems
- A basis set formed only of Slater-type functions or orbitals
- A basis set formed only of Gaussian-type functions or orbitals
Difference between the Slater-type functions and the Gaussian-type functions:
- The Slater-type functions have a physical meaning but are very difficult to calculate.
- The Gaussian-type functions have no physical meaning but are easy to calculate.
The solution:
Create a Slater-type functions as an expansion of Gaussian-type functions.
For more information check the following link:
http://www.helsinki.fi/kemia/fysikaalinen/opetus/jlk/luennot/Lecture5.pdf
Ex2: In solid systems
- A basis set formed only of the plane waves as in the pseudopoential methods
- A basis set formed of the plane waves and spherical harmonics as in the all-electron methos (ex: LAPW).
NB: In the scond case, to ensure the continuity at the sphere's surface, we have to proceed to expand the plane waves as an expansion of the spherical harmonics. Check this file at the page 19 http://susi.theochem.tuwien.ac.at/reg_user/textbooks/DFT_and_LAPW-2_cottenier.pdf
To get more information on the basis functions and the basis sets check the following links:
http://vergil.chemistry.gatech.edu/courses/chem6485/pdf/basis-sets.pdf
http://folk.uio.no/helgaker/talks/SostrupBasis_10.pdf
http://shodor.org/succeed-1.0/programs/compchem98/labs/settime/
Basis functions and basis sets in euclidean space
In euclidean space, we can use the vectors i,j and k to represent any vector in the plane or in the space. Thus, the three vectors are the basis vectors. To represent any vector in a plane, we need only two vectors i and j or i and k or j and k; so the basis set is formed only of two vectors. and to represent a vector in the space, we need the three vectors; so the basis set is formed of three vectors.
Third we talk about the DFT theory.
Eks: Kohn-Sham total energy Eks = T + V ----> (1)
T: Total cinetic energy (elctrons and nucleus) T = Te + Tn -----> (2)
Tn = 0 ------> (3) according to Born-Openheimer Approximation
V: total potential energy (electrons and nucleus ) V = Ve + Vn -----> (4)
Vn = Vext ------> (5) is called the exterior potential energy
Eh: Hartree total energy Eh = To + Vh ------> (6)
To: Total energy of non-intercting electrons Vh: Hartree potential energy (partial correlation contribution)
Ehf: Hartree-Fock total energy Ehf = To + Vh + Vx ----> (7)
Vx: Fock Exchange potential energy Ehf = Eh + Vx -----> (8)
From the equations (1), (2), (3) and (4) we get the following equation:
Eks = Te + Ve + Vext ------> (9)
Relation between Eks and Ehf
Eks = Ehf + Vc + Vext ------> (10)
Vc: Part of correlation which is absent in Hartree potential energy
From (9) and (10) we get the following rquation:
Eks = To + Vh + Vx + Vc + Vext -----------> (11)
We put Vxc = Vx + Vc ------> (12)
Vxc: is called Exchange-Correlation Energy
Vc: Correlation energy and is a kinetic energy in reality.
Vx: Exchange energy and is a potential energy and in reality is a correlation effect due to the Pauli exclusion principle which exclude the elctrons with the same spin to be in the same orbital.
NB: The meaning of correlation and exchange is convential and not real.
We put Veff = Vh + Vxc + Vext -------> (13)
Veff: is called the effective potential energy despite it contains some of the kinetic energy of correlation.
From (11), (12) and (13) we get the following equation:
Eks = To + Veff -------> (14)
From (9) and (11) we get that Vc = Te - To ----> (15)
and Vx = Ve - Vh ------> (16)
We know, according to the DFT theory, that all of the energies are related to the electron density; thus the final equation will be as follows:
Eks(rho) = To(rho) + Vh(rho) + Vxc(rho) + Vext(rho) --- > (17)
The exact ground state electron dnsity can be formulated as follows:
where the single-particle wave functions φi(~r) are the N lowest-energy solutions of the KohnSham equation:
And now we did won a lot. To find the ground-state density, we don’t need to use the second Hohenberg-Kohn theorem any more, but we can rely on solving familiar Schr¨odinger-like noninteracting single-particle equations. The alternative of using the regular Schr¨odinger equation, would have led to a far more difficult system of coupled differential equations, because of the electron-electron interaction.
Be aware that the single-particle wave functions φi are not the wave functions of electrons! They describe mathematical quasi-particles, without a direct physical meaning. Only the overall density of these quasi-particles is guaranteed to be equal to the true electron density. Also the single-particle energies ²i are not single-electron energies.
-----------------------------------------------------------------------------------------------------------
The previous statement is similar to what happennes in the superposition theorem in electrical circuits.
The real current is i1 and both i1(prime) and i1(second) are virtal currents which allow to calculate the real current.
reference: https://circuitglobe.com/what-is-superposition-theorem.html
--------------------------------------------------------------------------
Both the Hartree operator VH and the exchange-correlation operator Vxc depend on the density ρ(~r), which in turn depends on the φi which are being searched. This means we are dealing with a self-consistency problem: the solutions (φi) determine the original equation (VH and Vxc in HKS), and the equation cannot be written down and solved before its solution is known. An iterative procedure is needed to escape from this paradox (see fig. 1.1). Some starting density ρ0 is guessed, and a hamiltonian HKS1 is constructed with it. The eigenvalue problem is solved, and results in a set of φ1 from which a density ρ1 can be derived. Most probably ρ0 will differ from ρ1. Now ρ1 is used to construct HKS2, which will yield a ρ2, etc. The procedure can be set up in such a way that this series will converge to a density ρf which generates a HKSf which yields as solution again ρf : this final density is then consistent with the hamiltonian.
Reference: http://susi.theochem.tuwien.ac.at/reg_user/textbooks/DFT_and_LAPW-2_cottenier.pdf
The exchange-correlation functional
The exchange-correlation part is the only unknown one in the Schrondinger equation. To calculate it, we need to make approximations. The most known approwimations are:
- Local Density Approximation (LDA):
This postulate is somehow reasonable: it means that the exchange-correlation energy due to a particular density ρ(~r) could be found by dividing the material in infinitesimally small volumes with a constant density. Each such volume contributes to the total exchange correlation energy by an amount equal to the exchange correlation energy of an identical volume filled with a homogeneous electron gas, that has the same overall density as the original material has in this volume (see Fig. 1.2). No law of nature guarantees that the true Exc is of this form, it is only a reasonable guess. By construction, LDA is expected to perform well for systems with a slowly varying density. But rather surprisingly, it appears to be very accurate in many other (realistic) cases too.
- Generalized Gradient Approximation (GGA):
A next logical step to improve on LDA, is to make the exchange-correlation contribution of every infinitesimal volume not only dependent on the local density in that volume, but also on the density in the neighbouring volumes. In other words, the gradient of the density will play a role. Although GGA performs in general slightly better than LDA, there are a few drawbacks. There is only one LDA exchange-correlation functional, because there is a unique definition for ²xc. But there is some freedom to incorporate the density gradient, and therefore several versions of GGA exist (first drawback). Moreover, in practice one often fits a candidate GGA-functional with (hopefully only a few) free parameters to a large set of experimental data on atoms and molecules. The best values for these parameters are fixed then, and the functional is ready to be used routinely in solids. Therefore such a GGA-calculation is strictly spoken not an ab initio calculation, as some experimental information is used (second drawback). Nevertheless, there exist GGA’s that are parameter free.
Reference: http://susi.theochem.tuwien.ac.at/reg_user/textbooks/DFT_and_LAPW-2_cottenier.pdf
Fourth we talk about how to solve the Schrodinger equations
We call Hˆsp the single-particle hamiltonian. For HF, Vα is the exchange operator. The φm are true one-electron (or single-particle) orbitals for HF. Exchange is treated exactly, but correlation effects are not included at all. They can be added only in elaborations on the HF-method.
For DFT, Vα is the exchange-correlation operator, in the L(S)DA, GGA or another approximation. Exchange and correlation are both treated, but both approximately. The φm are mathematical single-particle orbitals (they are called quasi-particle orbitals).
The similarity between the Hartree-Fock and Kohn-Sham equations means that the same mathematical techniques can be used to solve them. ‘Solving’ in most methods means that we want to find the coefficients c m p needed to express φm in a given basis set φ b p :
The wave functions φm belong to a function space which has an infinite dimension, P is therefore in principle infinite. In practice one works with a limited set of basis functions. Such a limited basis will never be able to describe φm exactly, but one could try to find a basis that can generate a function that is ‘close’ to φm.
Continue reading on the page 9 of the following text book:
http://susi.theochem.tuwien.ac.at/reg_user/textbooks/DFT_and_LAPW-2_cottenier.pdf
Fiveth we talk about the different methods to solve the Kohn-Sham equations
A- The pseudopotential method
This method is based upon the Frozen-Core Approximation. In this approach, we treat the core electrons with a pseudopotential and the valence electrons with the plane waves. The plane waves are the best basis functions for the valence electrons but they need the use of the pseudopotentials because they didn't work with the core electrons.
For more information check the following links:
http://susi.theochem.tuwien.ac.at/reg_user/textbooks/DFT_and_LAPW-2_cottenier.pdf
http://helper.ipam.ucla.edu/publications/maws3/maws3_6085.pdf
For more information check the following links:
http://susi.theochem.tuwien.ac.at/reg_user/textbooks/DFT_and_LAPW-2_cottenier.pdf
http://helper.ipam.ucla.edu/publications/maws3/maws3_6085.pdf
https://th.fhi-berlin.mpg.de/th/Meetings/FHImd2001/pehlke1.pdf
http://www.lsr.nectec.or.th/images/e/e9/DFT_lecture_abinitworkshop.pdf
http://www.lsr.nectec.or.th/images/e/e9/DFT_lecture_abinitworkshop.pdf
B- The All-electrons methods
Unlike the Pseudopotetial method which calculate only the valence electrons only, the All-electrons methods calculate the both the core and valence electrons. There are many all-electron methods; we focused those used in the wien2k code.
The APW-method itself is of no practical use any more today. But for didactical reasons
it is advantageous to discuss APW first, before going to its successors, LAPW and APW+lo.
The ideas that lead to the APW basis set are very similar to what made us to introduce the pseudopotential. In the region far away from the nuclei, the electrons are more or less ‘free’. Free electrons are described by plane waves1 . Close to the nuclei, the electrons behave quite as they were in a free atom, and they could be described more efficiently by atomic like functions. Space is therefore divided now in two regions: around each atom2 a sphere with radius Rα is drawn (call it Sα). Such a sphere is often called a muffin tin sphere, the part of space occupied by the spheres is the muffin tin region. The remaining space outside the spheres is called the interstitial region (call it I). One augmented plane wave (APW) used in the expansion of ψ n ~k is defined as:
Note that the APW basis set is ~k-dependent, as was the plane wave basis set. The position inside the spheres is given with respect to the center of each sphere by ~r 0 = ~r −~rα (see fig. 3). The A α,~k+K~ `m are yet undetermined parameters, as is E. The latter has the dimension of energy.
The u α ` are solutions to the radial part of the Schr¨odinger equation for a free atom α, and this at the energy E. For a true free atom, the boundary condition that u α ` (r, E) should vanish for r → ∞, limits the number of energies E for which a solution u α ` can be found. But as this boundary condition does not apply here, we can find a numerical solution for any E. Hence, the u α ` themselves do not correspond to something physical, but that doesn’t harm: they are only part of a basis function, not of the searched eigenfunction itself. And because they are close to how the actual eigenfunction will look like in that region of the crystal, they will do their job as basis function very efficiently.
If an eigenfunction would be discontinuous, its kinetic energy would not be well-defined. Such a situation can therefore never happen, and we have to require that the plane wave outside the sphere matches the function inside the sphere over the complete surface of the sphere (in value, not in slope). That seems a weird thing to do: a plane wave is oscillating and has a unique direction built in, how can it match another function based on spherical harmonics over the entire surface of a sphere? To see how this is possible, we expand the plane wave in spherical harmonics about the origin of the sphere of atom α:
j`(x) is the Bessel function of order `. Requiring this at the sphere boundary (where ~r 0 = R~ α, which defines R~ α) to be equal to the `m-part of Eq. 3.1 easily yields:
This uniquely defines the A α,~k+K~ `m , apart from the still undetermined E. In principle there are an infinite number of terms in Eq. 3.2, which would force us to use an infinite number of A α,~k+K in order to create the matching. In practice we will have to truncate at some value `max . The cut-off for the plane waves (Kmax ) and for the angular functions (`max ) are of comparable quality if the number of nodes per unit of length is identical. This yields the condition RαKmax = `max . This allows to determine a good `max for a given Kmax . A finite value for `max means that for each APW the matching at the sphere boundaries will not be exact, but good enough to work with. It is not useful to make `max larger than the condition RαKmax requires, as it would lead to unstable behaviour at the sphere boundary (you can compare this with fitting a polynomial of high order through a limited number of points: the fit will be ‘perfect’, but not very meaningful). Therefore, it is also clear now that the muffin tin radii for the different atoms should not be too different: if they were, a value for `max that is suitable for each atom would not exist.
Now you should be able to visualize the meaning of a single APW φ ~k K~ (~r, E) of equation 3.1: it is an oscillating function that runs through the unit cell. Whenever it encounters an atom on its path, the simple oscillating behaviour is changed into something more complex inside the muffin tin sphere of that atom. Nevertheless, the function values inside and outside the sphere smoothly match, which is taken care of by a set of P`max `=1 2`max + 1 coefficients A α,~k+K~ `m that is different for each atom (the atom determines α, the APW under consideration determines ~k and K~ , all ` up to `max are present, with the corresponding values of m).
The ideas that lead to the APW basis set are very similar to what made us to introduce the pseudopotential. In the region far away from the nuclei, the electrons are more or less ‘free’. Free electrons are described by plane waves1 . Close to the nuclei, the electrons behave quite as they were in a free atom, and they could be described more efficiently by atomic like functions. Space is therefore divided now in two regions: around each atom2 a sphere with radius Rα is drawn (call it Sα). Such a sphere is often called a muffin tin sphere, the part of space occupied by the spheres is the muffin tin region. The remaining space outside the spheres is called the interstitial region (call it I). One augmented plane wave (APW) used in the expansion of ψ n ~k is defined as:
Note that the APW basis set is ~k-dependent, as was the plane wave basis set. The position inside the spheres is given with respect to the center of each sphere by ~r 0 = ~r −~rα (see fig. 3). The A α,~k+K~ `m are yet undetermined parameters, as is E. The latter has the dimension of energy.
The u α ` are solutions to the radial part of the Schr¨odinger equation for a free atom α, and this at the energy E. For a true free atom, the boundary condition that u α ` (r, E) should vanish for r → ∞, limits the number of energies E for which a solution u α ` can be found. But as this boundary condition does not apply here, we can find a numerical solution for any E. Hence, the u α ` themselves do not correspond to something physical, but that doesn’t harm: they are only part of a basis function, not of the searched eigenfunction itself. And because they are close to how the actual eigenfunction will look like in that region of the crystal, they will do their job as basis function very efficiently.
If an eigenfunction would be discontinuous, its kinetic energy would not be well-defined. Such a situation can therefore never happen, and we have to require that the plane wave outside the sphere matches the function inside the sphere over the complete surface of the sphere (in value, not in slope). That seems a weird thing to do: a plane wave is oscillating and has a unique direction built in, how can it match another function based on spherical harmonics over the entire surface of a sphere? To see how this is possible, we expand the plane wave in spherical harmonics about the origin of the sphere of atom α:
j`(x) is the Bessel function of order `. Requiring this at the sphere boundary (where ~r 0 = R~ α, which defines R~ α) to be equal to the `m-part of Eq. 3.1 easily yields:
This uniquely defines the A α,~k+K~ `m , apart from the still undetermined E. In principle there are an infinite number of terms in Eq. 3.2, which would force us to use an infinite number of A α,~k+K in order to create the matching. In practice we will have to truncate at some value `max . The cut-off for the plane waves (Kmax ) and for the angular functions (`max ) are of comparable quality if the number of nodes per unit of length is identical. This yields the condition RαKmax = `max . This allows to determine a good `max for a given Kmax . A finite value for `max means that for each APW the matching at the sphere boundaries will not be exact, but good enough to work with. It is not useful to make `max larger than the condition RαKmax requires, as it would lead to unstable behaviour at the sphere boundary (you can compare this with fitting a polynomial of high order through a limited number of points: the fit will be ‘perfect’, but not very meaningful). Therefore, it is also clear now that the muffin tin radii for the different atoms should not be too different: if they were, a value for `max that is suitable for each atom would not exist.
Now you should be able to visualize the meaning of a single APW φ ~k K~ (~r, E) of equation 3.1: it is an oscillating function that runs through the unit cell. Whenever it encounters an atom on its path, the simple oscillating behaviour is changed into something more complex inside the muffin tin sphere of that atom. Nevertheless, the function values inside and outside the sphere smoothly match, which is taken care of by a set of P`max `=1 2`max + 1 coefficients A α,~k+K~ `m that is different for each atom (the atom determines α, the APW under consideration determines ~k and K~ , all ` up to `max are present, with the corresponding values of m).
At first sight, it looks like we can now use the APW’s as a basis set, and proceed in the same way as for the plane wave basis set in order to determine the coefficients c
n,~k
K~
in the expansion
of the searched eigenfunction. However, this does not work. We did not settle the parameter E
yet. It turns out that in order to describe an eigenstate ψ
n
~k
(~r) accurately with APW’s, one has
to set E equal to the eigenvalue (or band energy) ²
n
~k
of that state. But this is exactly what we
are trying to determine! We are hence forced to start with a guessed value for ²
n
~k
and take this
as E. Now we can determine the APW’s, and construct the hamiltonian matrix elements and
overlap matrix (the APW’s are not orthogonal). The secular equation is determined, and our
guessed ²
n
~k
should be a root of it. Usually it is not, hence we have to try a second guess. Due
to this new E, the APW’s have to be determined again, and similarly for all matrix elements.
With the help of root determination algorithms, this guessing continues until a root – say ²
(n=1)
~k
– is found. And then the whole procedure starts over for ²
(n=2)
~k
, etc. (see fig. 3 for a suggestive
visualization of the roots of a secular equation, and fig. 3 for a flow chart of the APW method).
In practice, Kmax ≈ 3.5 au−1
is needed for sufficient accuracy. This is less than the typical
value of 5.5 for plane waves and pseudopotentials. As on page 12, the basis set size can be
estimated to be about P = 131 for APW, compared to roughly P = 270 for plane waves. The
calculation time (mainly determined by matrix diagonalization) scales with the third power
of the basis set size, which would suggest APW to be 10 times faster than pseudopotentials.
However, with a plane wave basis set, P eigenvalues are found by a single diagonalization, while
with APW one diagonalization is needed for every eigenvalue. This makes the APW method
inherently slow, much slower than the pseudopotential method.
The LAPW Method:



















No comments