Lagrangian and Hamiltonian Mechanics

Lagrange has perhaps done more than any other to give extent and harmony to such deductive researches by showing that the most varied consequences … may be derived from one radical formula, the beauty of the method so suiting the dignity of the results as to make his great work a kind of scientific poem.                                                                                               W. R. Hamilton

According to Newton's laws, the incremental work dW done by a force f on a particle moving an incremental distance dx, dy, dz in 3-dimensional space is given by the dot product

Now suppose the particle is constrained in such a way that its position has only two degrees of freedom. In other words, there are two generalized position coordinates X and Y such that the position coordinates x, y, and z of the particle are each strictly functions of these two generalized coordinates. We can then define a generalized force F with the components FX and FY such that

The total differentials of x, y, and z are then given by

Substituting these differentials into (1) and collecting terms by dX and dY, we have

Comparing this with (2), we see that the generalized force components are given by

Now, according to Newton's second law of motion, the individual components of force for a particle of mass m are

Substituting into the expression for FX gives

and similarly for FY.  Notice that the first product on the right side can be expanded as

and similarly for the other two products. Since x and X are both strictly functions of t, it follows that partial differentiation with respect to t is the same as total differentiation, and so the order of differentiation in the right-most term of (4) can be reversed (because partial differentiation is commutative). Hence (4) can be written as

Substituting this (and the corresponding expressions for the other two products) into equation (3), we get

Variations in x,y,z and X at constant t are independent of t (since each of these variables is strictly a function of t), so we have

Making these substitutions into (5) gives

Each term now contains an expression of the form r(∂r/∂s), which can also be written as ∂(r2/2)/∂s, so the overall expression can be re-written as

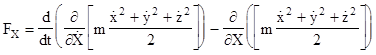To continue reading click on the following link:

https://www.mathpages.com/home/kmath523/kmath523.htm