The Wave Mechanics of an Atom with a Non-Coulomb Central Field (Hartree 1927 )

 D. R. Hartree

 Ph.D.,St John's College.

 

Part I. Theory and Methods

 Received 19 November, read 21 November, 1927.

 § 1. Introduction. 

On the theory of atomic structure proposed by Bohr, in whichthe electrons are considered as point charges revolving in orbitsabout the nucleus, the Orbits being specified by quantum con-ditions, it is well known that both a qualitative and an approximatequantitative explanation of many features of the simpler opticalspectra and of X-ray spectra of atoms with many electrons (e.g.Rydberg sequences in optical spectra, term magnitudes in bothX-ray and optical spectra) can be given, if the assumption is madethat the effects of the electrons on one another can be representedby supposing each to move in a central non-Coulomb field of force*;further, the additional concept of a spinning electron provides asimilar explanation of other features of these specbraf (e.g.doublet struoture of terms and magnitude of doublet separation,anomalous Zeeman effect). This assumption of a central field wasadmittedly a rough approximation made in the absence of anydetailed ideas about the interaction between the different electronsin an atom, but in view of its success as a first approximation for theorbital atom model, the question arises whether, the same simpleapproximations may not give useful results when applied to thenew formulation of the quantum theory which has been developedin the last two years.

 https://sci-hub.se/10.1017/S0305004100011919

Part II. Some Results and Discussion

 Received 19 November, read 21 November, 1927

Abstract

The methods of solution of the wave equation for a central field given in the previous paper are applied to various atoms. For the core electrons, the details of the interaction of the electrons in a single nk group are neglected, but an approximate correction is made for the fact that the distributed charge of an electron does not contribute to the field acting on itself (§2).

For a given atom the object of the work is to find a field such that the solutions of the wave equation for the core electrons in this field (corrected as just mentioned for each core electron) give a distribution of charge which reproduces the field. This is called the self-consistent field, and the process of finding it is one of successive approximation (§ 3).

Approximations to the self-consistent field have been found for He (§ 4), Rb+ (§ 5), Na+, Cl− (§ 9). For He the energy parameter for the solution of the wave equation for one electron in the self-consistent field of the nucleus and the other corresponds to an ionisation potential of 24·85 volts (observed 24·6 volts); this agreement suggests that for other atoms the values of the energy parameter in the self-consistent field (corrected for each core electron) will probably give good approximations to the X-ray terms (§4).

The most extensive work has been carried out for Rb+. The distribution of charge given by the wave functions in the self-consistent field is compared with the distribution calculated by other methods (§ 6). The values of X-ray and optical terms calculated from the self-consistent field show satisfactory agreement with those observed (§ 7).

The wave mechanical analogue of the case in which on the orbital model an internal and an external orbit of the same energy are possible is discussed (§ 8).

---

 https://sci-hub.se/https://doi.org/10.1017/S0305004100011920

 

 

Part III. Term Values and Intensities in Series in Optical Spectra

 

In two recent papers the writer has given an account of a practical method of finding the characteristic values and functions of Schrödinger's wave equations for a given non-Coulomb central field. For terms of optical spectra the method is effectively the following. We take the wave equation in the form

and require the values of ɛ for the solutions which are zero at the origin and at r = ∞. We consider the result of integrating this equation outwards from P = 0 at r = 0 to a radius r0 at which the deviation from a Coulomb field is negligible, and inwards from P = 0 at r = ∞ to the same radius, with a given value of ɛ; the characteristic values are those values for which these two solutions join smoothly on to one another, i.e. for which they have the same value of η = −P′/P at this radius. For a given ɛ, the solution zero at the origin depends on the particular atom; the solution zero at infinity can be expressed in a form independent of any particular atom.

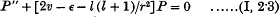
 https://sci-hub.se/https://doi.org/10.1017/S0305004100015954